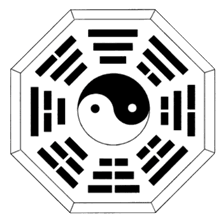
Théorie de numération binaire tirée du Yi-King
Les Européens ont une si haute opinion de leur science qu’ils en croient le prestige irrésistible, et ils s’imaginent que les autres peuples doivent tomber en admiration devant leurs découvertes les plus insignifiantes ; cet état d’esprit, qui les conduit parfois à de singulières méprises, n’est pas tout nouveau, et nous en avons trouvé chez Leibnitz un exemple assez amusant. On sait que ce philosophe avait formé le projet d’établir ce qu’il appelait une « caractéristique universelle », c’est-à-dire une sorte d’algèbre généralisée, rendue applicable aux notions de tout ordre, au lieu d’être restreinte aux seules notions quantitatives ; cette idée lui avait d’ailleurs été inspirée par certains auteurs du moyen âge, notamment Raymond Lulle et Trithème. Or, au cours des études qu’il fit pour essayer de réaliser ce projet, Leibnitz fut amené à se préoccuper de la signification des caractères idéographiques qui constituent l’écriture chinoise, et plus particulièrement des figures symboliques qui forment la base du Yi-king ; on va voir comment il comprit ces dernières : « Leibnitz, dit L. Couturat, croyait avoir trouvé par sa numération binaire (numération qui n’emploie que les signes 0 et 1, et dans laquelle il voyait une image de la création ex nihilo) l’interprétation des caractères de Fo-hi, symboles chinois mystérieux et d’une haute antiquité, dont les missionnaires européens et les Chinois eux-mêmes ne connaissaient pas le sens... Il proposait d’employer cette interprétation à la propagation de la foi en Chine, attendu qu’elle était propre à donner aux Chinois une haute idée de la science européenne, et à montrer l’accord de celle-ci avec les traditions vénérables et sacrées de la sagesse chinoise. Il joignit cette interprétation à l’exposé de son arithmétique binaire qu’il envoya à l’Académie des Sciences de Paris » [1]. Voici, en effet, ce que nous lisons textuellement dans le mémoire dont il est ici question : « Ce qu’il y a de surprenant dans ce calcul (de l’Arithmétique binaire), c’est que cette Arithmétique par 0 et 1 se trouve contenir le mystère des lignes d’un ancien Roi et Philosophe nommé Fohy, qu’on croit avoir vécu il y a plus de quatre mille ans [2] et que les Chinois regardent comme le Fondateur de leur Empire et de leurs sciences. Il y a plusieurs figures linéaires qu’on lui attribue, elles reviennent toutes à cette Arithmétique ; mais il suffit de mettre ici la Figure de huit Cova [3], comme on l’appelle, qui passe pour fondamentale, et d’y joindre l’explication qui est manifeste, pourvu qu’on remarque premièrement qu’une ligne entière signifie l’unité ou 1, et secondement qu’une ligne brisée signifie le zéro ou 0. Les Chinois ont perdu la signification des Cova ou Linéations de Fohy, peut-être depuis plus d’un millénaire d’années, et ils ont fait des commentaires là-dessus, où ils ont cherché je ne sçai quels sens éloignés, de sorte qu’il a fallu que la vraie explication leur vînt maintenant des Européens. Voici comment : il n’y a guères plus de deux ans que j’envoyai au R. P. Bouvet, Jésuite français célèbre, qui demeure à Pékin, ma manière de compter par 0 et 1, et il n’en fallut pas davantage pour lui faire reconnoître que c’est la clef des figures de Fohy. Ainsi, m’écrivant le 14 novembre 1701, il m’a envoyé la grande figure de ce Prince Philosophe qui va à 64 [4], et ne laisse plus lieu de douter de la vérité de notre interprétation, de sorte qu’on peut dire que ce Père a déchiffré l’énigme de Fohy, à l’aide de ce que je lui avois communiqué. Et comme ces figures sont peut-être le plus ancien monument de science qui soit au monde, cette restitution de leur sens, après un si grand intervalle de tems, paroîtra d’autant plus curieuse... Et cet accord me donne une grande opinion de la profondeur des méditations de Fohy. Car ce qui nous paroît aisé maintenant, ne l’étoit pas tout dans ces tems éloignés... Or, comme l’on croit à la Chine que Fohy est encore auteur des caractères chinois, quoique fort altérés par la suite des tems, son essai d’Arithmétique fait juger qu’il pourroit bien s’y trouver encore quelque chose de considérable par rapport aux nombres et aux idées, si l’on pouvoît déterrer le fondement de l’écriture chinoise, d’autant plus qu’on croit à la Chine qu’il a eu égard aux nombres en l’établissant. Le R. P. Bouvet est fort porté à pousser cette pointe, et très capable d’y réussir en bien des manières. Cependant je ne sçai s’il y a jamais eu dans l’écriture chinoise un avantage approchant de celui qui doit être nécessairement dans une Caractéristique que je projette. C’est que tout raisonnement qu’on peut tirer des notions, pourroit être tiré de leurs Caractères par une manière de calcul, qui seroit un des plus importans moyens d’aider l’esprit humain » [5]. Nous avons tenu à reproduire tout au long ce curieux document, qui permet de mesurer jusqu’où pouvait aller la compréhension de celui que nous regardons pourtant comme le plus « intelligent » de tous les philosophes modernes : Leibnitz était persuadé à l’avance que sa « caractéristique », qu’il ne parvint d’ailleurs jamais à constituer (et les « logisticiens » d’aujourd’hui ne sont guère plus avancés), ne pourrait manquer d’être bien supérieure à l’idéographie chinoise ; et le plus beau, c’est qu’il pense faire grand honneur à Fo-hi en lui attribuant un « essai d’arithmétique » et la première idée de son petit jeu de numération. Il nous semble voir d’ici le sourire des Chinois, si on leur avait présenté cette interprétation quelque peu puérile, qui aurait été fort loin de leur donner « une haute idée de la science européenne », mais qui aurait été propre à leur en faire apprécier très exactement la portée réelle. La vérité est que les Chinois n’ont jamais « perdu la signification », ou plutôt les significations des symboles dont il s’agit ; seulement, ils ne se croyaient point obligés de les expliquer au premier venu, surtout s’ils jugeaient que ce serait peine perdue ; et Leibnitz, en parlant de « je ne sçai quels sens éloignés », avoue en somme qu’il n’y comprend rien. Ce sont ces sens, soigneusement conservés par la tradition (que les commentaires ne font que suivre fidèlement) qui constituent « la vraie explication », et ils n’ont d’ailleurs rien de « mystique » ; mais quelle meilleure preuve d’incompréhension pouvait-on donner que de prendre des symboles métaphysiques pour « des caractères purement numéraux » ? Des symboles métaphysiques, voilà en effet ce que sont essentiellement les « trigrammes » et les « hexagrammes », représentation synthétique de théories susceptibles de recevoir des développements illimités, et susceptibles aussi d’adaptations multiples, si, au lieu de se tenir dans le domaine des principes, on en veut faire l’application à tel ou tel ordre déterminé. On aurait fort étonné Leibnitz si on lui avait dit que son interprétation arithmétique trouvait place aussi parmi ces sens qu’il rejetait sans les connaître, mais seulement à un rang tout à fait accessoire et subordonné ; car cette interprétation n’est pas fausse en elle-même, et elle est parfaitement compatible avec toutes les autres, mais elle est tout à fait incomplète et insuffisante, insignifiante même quand on l’envisage isolément, et ne peut prendre d’intérêt qu’en vertu de la correspondance analogique qui relie les sens inférieurs au sens supérieur, conformément à ce que nous avons dit de la nature des « sciences traditionnelles ». Le sens supérieur, c’est le sens métaphysique pur ; tout le reste, ce ne sont qu’applications diverses, plus ou moins importantes, mais toujours contingentes : c’est ainsi qu’il peut y avoir une application arithmétique comme il y en a une indéfinie d’autres, comme il y a par exemple une application logique, qui eût pu servir davantage au projet de Leibnitz s’il l’eût connue, comme il y a une application sociale, qui est le fondement du Confucianisme, comme il y a une application astronomique, la seule que les Japonais aient jamais pu saisir [6], comme il y a même une application divinatoire, que les Chinois regardent d’ailleurs comme une des plus inférieures de toutes, et dont ils abandonnent la pratique aux jongleurs errants. Si Leibnitz s’était trouvé en contact direct avec les Chinois, ceux-ci lui auraient peut-être expliqué (mais l’aurait-il compris ?) que même les chiffres dont il se servait pouvaient symboliser des idées d’un ordre beaucoup plus profond que les idées mathématiques, et que c’est en raison d’un tel symbolisme que les nombres jouaient un rôle dans la formation des idéogrammes, non moins que dans l’expression des doctrines pythagoriciennes (ce qui montre que ces choses n’étaient pas ignorées de l’antiquité occidentale). Les Chinois auraient même pu accepter la notation par 0 et 1, et prendre ces « caractères purement numéraux » pour représenter symboliquement les idées métaphysiques du yin et du yang (qui n’ont d’ailleurs rien à voir avec la conception de la création ex nihilo), tout en ayant bien des raisons de préférer, comme plus adéquate, la représentation fournie par les « linéations » de Fo-hi, dont l’objet propre et direct est dans le domaine métaphysique. Nous avons développé cet exemple parce qu’il fait apparaître clairement la différence qui existe entre le systématisme philosophique et la synthèse traditionnelle, entre la science occidentale et la sagesse orientale ; il n’est pas difficile de reconnaître, sur cet exemple qui a pour nous, lui aussi, une valeur de symbole, de quel côté se trouvent l’incompréhension et l’étroitesse de vues [7]. Leibnitz, prétendant comprendre les symboles chinois mieux que les Chinois eux-mêmes, est un véritable précurseur des orientalistes, qui ont, les Allemands surtout, la même prétention à l’égard de toutes les conceptions et de toutes les doctrines orientales, et qui refusent de tenir le moindre compte de l’avis des représentants autorisés de ces doctrines : nous avons cité ailleurs le cas de Deussen s’imaginant expliquer Shankarâchârya aux Hindous, et l’interprétant à travers les idées de Schopenhauer ; ce sont bien là des manifestations d’une seule et même mentalité.
---
[1] La Logique de Leibnitz, pp.474-475.
[2] La date exacte est 3468 avant l’ère chrétienne, d’après une chronologie basée sur la description précise de l’état du ciel à cette époque ; ajoutons que le nom de Fo-hi sert en réalité de désignation à toute une période de l’histoire chinoise.
[3] Kova est le nom chinois des « trigrammes », c’est-à-dire des figures qu’on obtient en assemblant trois à trois, de toutes les manières possibles, des traits pleins et brisés, et qui sont effectivement au nombre de huit.
[4] Il s’agit là des soixante-quatre « hexagrammes » de Wen-wang, c’est-à-dire des figures de six traits formés en combinant les huit « trigrammes » deux à deux. Notons en passant que l’interprétation de Leibnitz est tout à fait incapable d’expliquer, entre autres choses, pourquoi ces « hexagrammes », aussi bien que les « trigrammes » dont ils sont dérivés, sont toujours disposés en un tableau de forme circulaire.
[5] Explication de l’Arithmétique binaire, qui se sert des seuls caractères 0 et 1, avec des remarques sur son utilité, et sur ce qu’elle donne le sens des anciennes figures chinoises de Fohy, Mémoire de l’Académie des Sciences, 1703 : OEuvres mathématiques de Leibnitz, éd. Gerhardt, t. VII, pp. 226-227. Ŕ Voir aussi De Dyadicis : ibid., t. VII, pp. 233-234. Ce texte se termine ainsi : « Ita mirum accidit, ut res ante ter et amplius (millia !) annos nota in extremo noetri continentis, oriente, nunc in extreme ejus occidente, sed melioribus, ut spero auspiciis resuscitaretur. Nam non apparet, antea usum hujus characterismi ad augendam numerotionem intelligentes nescio quos mysticos significatus in characteribus mere numeralibus sibi fingebant. »
[6] La traduction française du Yi-king par Philastre (Annales du Musée Guimet, t. VIII et t. XXIII), qui est d’ailleurs une oeuvre extrêmement remarquable, a le défaut d’envisager un peu trop exclusivement le sens astronomique.
[7] Nous rappellerons ici ce que nous avons dit de la pluralité de sens de tous les textes traditionnels, et spécialement des idéogrammes chinois : Introduction générale à l’étude des doctrines hindoues, 2e partie, ch. IX. Ŕ Nous y joindrons encore cette citation empruntée à Philastre : « En chinois, le mot (ou le caractère) n’a presque jamais de sens absolument défini et limité ; le sens résulte très généralement de la position dans la phrase, mais avant tout de son emploi dans tel ou tel livre plus ancien et de l’interprétation admise dans ce cas… Le mot n’a de valeur que par ses acceptions traditionnelles » (Yi-king, 1re partie, p. 8 ).
René Guénon, Orient et Occident (1924), chapitre II - La superstition de la science
Source :
http://martin-wagenschein.de/K-Kohl/Informat/Leibniz.htm
Les sources d'inspiration de Leibnitz
Ce qui nous concerne plus directement pour le moment, c’est ceci : si nous avons à constater de telles insuffisances chez Leibnitz, et des insuffisances d’autant plus graves qu’elles portent surtout sur les questions de principes, que pourra-t-il bien en être des autres philosophes et mathématiciens modernes, auxquels il est assurément très supérieur malgré tout ? Cette supériorité, il la doit, d’une part, à l’étude qu’il avait faite des doctrines scolastiques du moyen âge, bien qu’il ne les ait pas toujours entièrement comprises, et, d’autre part, à certaines données ésotériques, d’origine ou d’inspiration principalement rosicrucienne (1), données évidemment très incomplètes et même fragmentaires, et que d’ailleurs il lui arriva parfois d’appliquer assez mal, comme nous en verrons quelques exemples ici même ; c’est à ces deux « sources » pour parler comme les historiens, qu’il convient de rapporter, en définitive, à peu près tout ce qu’il y a de réellement valable dans ses théories, et c’est là aussi ce qui lui permit de réagir, quoique imparfaitement, contre le cartésianisme, qui représentait alors, dans le double domaine philosophique et scientifique, tout l’ensemble des tendances et des conceptions les plus spécifiquement modernes. Cette remarque suffit en somme à expliquer, en quelques mots, tout ce que fut Leibnitz, et, si on veut le comprendre, il ne faudrait jamais perdre de vue ces indications générales, que nous avons cru bon, pour cette raison, de formuler dès le début ; mais il est temps de quitter ces considérations préliminaires pour entrer dans l’examen des questions mêmes qui nous permettront de déterminer la véritable signification du calcul infinitésimal.
-----
1 - La marque indéniable de cette origine se trouve dans la figure hermétique placée par Leibnitz en tête de son traité De Arte combinatoria : c’est une représentation de la Rota Mundi, dans laquelle, au centre de la double croix des éléments (feu et eau, air et terre) et des qualités (chaud et froid, sec et humide), la quinta essentia est symbolisée par une rose à cinq pétales (correspondant à l’éther considéré en lui-même et comme principe des quatre autres éléments) ; naturellement, cette « signature » est passée complètement inaperçue de tous les commentateurs universitaires !
-----
1 - La marque indéniable de cette origine se trouve dans la figure hermétique placée par Leibnitz en tête de son traité De Arte combinatoria : c’est une représentation de la Rota Mundi, dans laquelle, au centre de la double croix des éléments (feu et eau, air et terre) et des qualités (chaud et froid, sec et humide), la quinta essentia est symbolisée par une rose à cinq pétales (correspondant à l’éther considéré en lui-même et comme principe des quatre autres éléments) ; naturellement, cette « signature » est passée complètement inaperçue de tous les commentateurs universitaires !
René Guénon, Les principes du calcul infinitésimal, Introduction
Leibnitz, un des scientifiques reconnus comme les plus brillants de notre époque, prenait ainsi les sources de son travail dans des résidus de connaissance traditionnelle. Sa démarche n'avait donc pas grand chose à voir avec la "démarche scientifique" creuse et dogmatique, qui n'est rien d'autre qu'un refus revendiqué de toute véritable connaissance. Il n'empêche, malgré sa valeur parmi les modernes, que la panacée qu'il a cru trouver dans son interprétation du symbolisme du Yi-King n'était rien de plus qu'une préfiguration de l'informatique, technique basée sur la quantité pure.
Une autre question se pose encore : la quantité se présente à nous sous des modes divers, et, notamment, il y a la quantité discontinue, qui est proprement le nombre[1], et la quantité continue, qui est représentée principalement par les grandeurs d’ordre spatial et temporel ; quel est, parmi ces modes, celui qui constitue plus précisément ce qu’on peut appeler la quantité pure ? Cette question a aussi son importance, d’autant plus que Descartes, qui se trouve au point de départ d’une bonne partie des conceptions philosophiques et scientifiques spécifiquement modernes, a voulu définir la matière par l’étendue, et faire de cette définition même le principe d’une physique quantitative qui, si elle n’était pas encore du « matérialisme », était du moins du « mécanisme » ; on pourrait être tenté de conclure de là que c’est l’étendue qui, étant directement inhérente à la matière, représente le mode fondamental de la quantité. Par contre, saint Thomas d’Aquin, en disant que « numerus stat ex parte materiæ », semble plutôt suggérer que c’est le nombre qui constitue la base substantielle de ce monde, et que c’est lui, par conséquent, qui doit être regardé véritablement comme la quantité pure ; ce caractère « basique » du nombre s’accorde d’ailleurs parfaitement avec le fait que, dans la doctrine pythagoricienne, c’est lui qui, par analogie inverse, est pris comme symbole des principes essentiels des choses. Il faut d’ailleurs remarquer que la matière de Descartes n’est plus la materia secunda des scolastiques, mais qu’elle est déjà un exemple, et peut-être le premier en date, d’une « matière » de physicien moderne, bien qu’il n’ait pas encore mis dans cette notion tout ce que ses successeurs devaient y introduire peu à peu pour en arriver aux théories les plus récentes sur la « constitution de la matière ». Il y a donc lieu de soupçonner qu’il peut y avoir, dans la définition cartésienne de la matière, quelque erreur ou quelque confusion, et qu’il a dû déjà s’y glisser, peut-être à l’insu de son auteur, un élément qui n’est pas d’ordre purement quantitatif ; et en effet, comme nous le verrons par la suite, l’étendue, tout en ayant évidemment un caractère quantitatif, comme d’ailleurs tout ce qui appartient au monde sensible, ne saurait pourtant être regardée comme pure quantité. De plus, on peut remarquer aussi que les théories qui vont le plus loin dans le sens de la réduction au quantitatif sont généralement « atomistes », sous une forme ou sous une autre, c’est-à-dire qu’elles introduisent dans leur notion de matière une discontinuité qui la rapproche beaucoup plus de la nature du nombre que de celle de l’étendue ; et même le fait que la matière corporelle ne peut pas malgré tout être conçue autrement que comme étendue n’est pour tout « atomisme » qu’une source de contradictions. Une autre cause de confusion en tout cela, et sur laquelle nous aurons à revenir, est l’habitude que l’on a prise de considérer « corps » et « matière » comme à peu près synonymes ; en réalité, les corps ne sont nullement la materia secunda, qui ne se rencontre nulle part dans les existences manifestées en ce monde, mais ils en procèdent seulement comme de leur principe substantiel. En définitive, c’est bien le nombre, qui, lui non plus, n’est jamais perçu directement et à l’état pur dans le monde corporel qui doit être considéré en premier lieu dans le domaine de la quantité, comme en constituant le mode fondamental ; les autres modes ne sont que dérivés, c’est-à-dire qu’ils ne sont en quelque sorte quantité que par participation au nombre, ce qu’on reconnaît d’ailleurs implicitement quand on considère, comme il en est toujours en fait, que tout ce qui est quantitatif doit pouvoir s’exprimer numériquement. Dans ces autres modes, la quantité, même si elle est l’élément prédominant, apparaît toujours comme plus ou moins mélangée de qualité, et c’est ainsi que les conceptions de l’espace et du temps, en dépit de tous les efforts des mathématiciens modernes, ne pourront jamais être exclusivement quantitatives, à moins que l’on ne consente à les réduire à des notions entièrement vides, sans aucun contact avec une réalité quelconque ; mais, à vrai dire, la science actuelle n’est-elle pas faite en grande partie de ces notions vides, qui n’ont plus que le caractère de « conventions » sans la moindre portée effective ? Nous nous expliquerons plus complètement sur cette dernière question, surtout en ce qui concerne la nature de l’espace, car ce point a un rapport étroit avec les principes du symbolisme géométrique, et, en même temps, il fournit un excellent exemple de la dégénérescence qui conduit des conceptions traditionnelles aux conceptions profanes ; et nous y arriverons en examinant tout d’abord comment l’idée de la « mesure », sur laquelle repose la géométrie elle-même, est, traditionnellement, susceptible d’une transposition qui lui donne une tout autre signification que celle qu’elle a pour les savants modernes, qui n’y voient en somme que le moyen d’approcher le plus possible de leur « idéal » à rebours, c’est-à-dire d’opérer peu à peu la réduction de toutes choses à la quantité.
-----
[1] La notion pure du nombre est essentiellement celle du nombre entier, et il est évident que la suite des nombres entiers constitue une série discontinue ; toutes les extensions que cette notion a reçues, et qui ont donné lieu à la considération des nombres fractionnaires et des nombres incommensurables, en sont de véritables altérations, et elles ne représentent en réalité que les efforts qui ont été faits pour réduire autant que possible les intervalles du discontinu numérique, afin de rendre moins imparfaite son application à la mesure des grandeurs continues.
-----
[1] La notion pure du nombre est essentiellement celle du nombre entier, et il est évident que la suite des nombres entiers constitue une série discontinue ; toutes les extensions que cette notion a reçues, et qui ont donné lieu à la considération des nombres fractionnaires et des nombres incommensurables, en sont de véritables altérations, et elles ne représentent en réalité que les efforts qui ont été faits pour réduire autant que possible les intervalles du discontinu numérique, afin de rendre moins imparfaite son application à la mesure des grandeurs continues.
René Guénon, Le Règne de la Quantité et les Signes des Temps, chapitre II - « Materia signata quantitate »
Si nous considérons l’ensemble de ce domaine de manifestation qu’est notre monde, nous pouvons dire que, à mesure qu’elles s’éloignent de l’unité principielle, les existences y deviennent d’autant moins qualitatives et d’autant plus quantitatives ; en effet, cette unité, qui contient synthétiquement en elle-même toutes les déterminations qualitatives des possibilités de ce domaine, en est le pôle essentiel, tandis que le pôle substantiel, dont on s’approche évidemment dans la même mesure qu’on s’éloigne de l’autre, est représenté par la quantité pure, avec l’indéfinie multiplicité « atomique » qu’elle implique, à l’exclusion de toute distinction autre que numérique entre ses éléments. Cet éloignement graduel de l’unité essentielle peut d’ailleurs être envisagé sous un double point de vue, en simultanéité et en succession ; nous voulons dire qu’on peut l’envisager, d’une part, dans la constitution des êtres manifestés, où ces degrés déterminent, pour les éléments qui y entrent ou les modalités qui leur correspondent, une sorte de hiérarchie, et, d’autre part, dans la marche même de l’ensemble de la manifestation du commencement à la fin d’un cycle ; il va de soi que, ici, c’est au second de ces deux points de vue que nous devons nous référer plus particulièrement. Dans tous les cas, on pourrait, à cet égard, représenter géométriquement le domaine dont il s’agit par un triangle dont le sommet est le pôle essentiel, qui est qualité pure, tandis que la base est le pôle substantiel, c’est-à-dire, pour ce qui est de notre monde, la quantité pure, figurée par la multiplicité des points de cette base, en opposition avec le point unique qu’est le sommet ; si l’on trace des parallèles à la base pour représenter les différents degrés de l’éloignement dont nous venons de parler, il est évident que la multiplicité qui symbolise le quantitatif y sera d’autant plus marquée qu’on s’éloignera davantage du sommet pour s’approcher de la base. Seulement, pour que le symbole soit aussi exact que possible, il faudrait supposer que la base est indéfiniment éloignée du sommet, d’abord parce que ce domaine de manifestation est véritablement indéfini lui-même, et ensuite pour que la multiplicité des points de la base soit pour ainsi dire portée à son maximum ; en outre, on indiquerait par là que cette base, c’est-à-dire la quantité pure, ne peut jamais être atteinte dans le cours du processus de manifestation, bien que celui-ci y tende sans cesse de plus en plus, et que, à partir d’un certain niveau, le sommet, c’est-à-dire l’unité essentielle ou la qualité pure, soit en quelque sorte perdu de vue, ce qui correspond précisément à l’état actuel de notre monde.
Ibid., chapitre VII - L’uniformité contre l’Unité